Grafik Fungsi Trigonometri

Daftar Isi

Periode Fungsi Trigonometri

Fungsi f dgn wilayah R dibilang periodik apabila ada bilangan $p \ne 0$ , sedemikian sehingga $f(x+p) = f(x)$ , dgn $x \epsilon R$ . Bilangan nyata p terkecil yg menyanggupi $f(x+p) = f(x)$ disebut periode dasar fungsi f.

Jika fungsi f periodik dgn periode dasar p, maka periode-periode dr fungsi f ialah $n \times p$ , dgn n yaitu bilangan asli. Jika f & g ialah fungsi yg periodik dgn periode p, maka $f+g$ & fg pula periodik dgn periode p.

Lihat pula materi Sosiologiku.com yang lain:

Kuartil, Desil, Simpangan Baku, & Varian

Persamaan Trigonometri

1. Periode fungsi sinus & kosinus

Untuk penambahan panjang busur $a$ dgn kelipatan $2\pi$ (satu putran sarat ) akan diperoleh titik p(a) yg sama, sehingga dengan-cara lazim berlaku :

$\sin (a+k \times 2\pi) = \sin a$ dgn k∈B atau

$\sin (a+k\times 360^ \circ ) = \sin a^ \circ$ dgn k∈B

$\cos (a+k\times 2\pi)$ dgn k∈B atau

$\cos (a+ k\times 360^ \circ )$ dgn k∈B

Dengan demikian, fungsi sinus $f(x) = \sin x$ vatau $f(x) = \sin x^ \circ$ & fungsi kosinus $f(x) = cos x$ atau $f(x) = cos x^ \circ$ adalah fungsi periodik dgn periode dasar $2\pi$ atau $360^ \circ$ .

grafik fungsi trigonometri sinus & cosinus

2. Periode fungsi tangen

Untuk penambahan panjang busur $a$ dgn kelipatan $\pi$ (setengah putran sarat ) akan diperoleh titik $p(a+k\times p)$ yg nilai tangennya sama untuk kedua sudut tersebut, sehingga dengan-cara umum $\tan (a + k \times \pi) = \tan a$ dgn $k \epsilon B$ atau $\tan (a+k\times 1806 \circ ) = \tan a^ \circ$ dgn $k \epsilon B$ .

grafik fungsi tangen

Dengan demikian tangen $f(x) = \tan x$ atau $f(x) = \tan^ \circ$ yaitu fungsi periodik dgn periode $\pi$ atau $180^ \circ$ .

grafik fungsi trigonometri lengkap

Dengan td yaitu tak didefinisikan. Untuk mempermudah, maka lihatlah segitiga berikut :

sudut istimewa segitiga

Dari desain segitiga tersebut diperoleh nilai setiap sudut $30^ \circ , 45^ \circ$ & $60^ \circ$ . Untuk sudut $0^ \circ$ & $90^ \circ$ diperoleh dgn cara berikut :

konsep segitiga trigonometri

Didapat :

$\sin a = \frac y r$

$cos a = \frac x r$

$\tan a = \frac y x$

Jika titik $P(x,y)$ bergerak mendekati sumbu X faktual, risikonya berimpit dgn sumbu X, maka x=r, y=0, $x = r,y = 0$ & $a^ \circ =0^ \circ$ , sehingga

$\sin 0^ \circ = \frac 0 r = 0$

$\cos 0^ \circ = \frac r r = 1$

$\tan 0^ \circ = \frac 0 r = 0$

Jika titik P(x,y) $P(x,y)$ bergerak mendekati sumbu Y konkret, kesannya berimpit dgn sumbu Y, maka

$x =0,y = r$ , & $a^ \circ = 90^ \circ$ , sehingga

$\sin 90^ \circ = \frac r r = 1$

$\cos 0^ \circ = \frac 0 r = 0$

tan⁡ $\tan 0^ \circ = \frac r 0$ = tak didefinisikan

Nilai Maksimum & Minimum Fungsi Trigonometri

Untuk setiap titik P(x,y) $P(x,y)$ pada fungsi trigonometri mempunyai relasi :

$-r \le x \le r$ & $-r \le y \le r$

$-1 \le \frac x r \le 1$ & $-1 \le \frac y r \le 1$

$-1 \le \cos a \le 1$ & $-1 \le \sin a \le 1$

Berdasarkan uraian tersebut mampu dikemukakan bahwa :

Nilai maksimum & minimum fungsi sinus

Fungsi sinus $y =f(x) = \sin x$ mempunyai nilai maksimum $y_ maks = 1$ yg diraih untuk $x =\frac 1 2 \pi + k \times 2\pi$ dgn $k \epsilon B$ & nilai minimum $y_ min = -1$ yg diraih untuk $x = \frac 3 2 \pi + k \times 2\pi$ dgn $k \epsilon B$ .

Fungsi sinus $y = f(x) = \sin x^ \circ$ mempunyai nilai maksimum $y_ maks = 1$ yg dicapai untuk $x = 90^ \circ + k \times 360^ \circ$ dgn $k \epsilon B$ & nilai minimum $y_ maks = -1$ yang diraih untuk $x = 270^ \circ + k \times 360^ \circ$ dengan $k \epsilon B$ .

Nilai maksimum & minimum fungsi kosinus

Fungsi kosinus $y = f(x) = \cos x$ memiliki nilai maksimum $y_ maks = 1$ yg dicapai untuk $x =k \times 2\pi$ dgn $k \epsilon B$ & nilai minimum $y_ min = -1$ yg diraih untuk $x = \pi + k \times 2\pi$ dgn $k \epsilon B$ .

Fungsi kosinus $y = f(x) = \cos x^ \circ$ mempunyai nilai maksimum $y_ maks = 1$ yg dicapai untuk $x = k \times 360^ \circ$ dgn $k \epsilon B$ & nilai minimum $y_ min = -1$ yg diraih untuk $x = 180^ \circ + k \times 360^ \circ$ dgn $k \epsilon B$ .

Secara biasa dapat dikemukakan bahwa :

Jika fungsi sinus $y = f(x) = a \sin (bx + c) + d$ , maka nilai maksimumnya $y_ maks = \mid a\mid + d$ & nilai minimumnya $y_ min = -\mid a\mid + d$

Jika fungsi kosinus $y = f(x) = a \cos (bx + c) + d$ , maka nilai maksimumnya $y_ maks = \mid a\mid + d$ & nilai minimumnya $y_ min = -\mid a\mid + d$

Jika $y = f(x)$ ialah fungsi periodik dgn nilai maksimum $y_ maks$ & minimum $y_ min$ , maka amplitudonya adalah :

$Amplitudo = \frac 1 2 (y_ maks - y_ min )$

Jenis Grafik Fungsi Trigonometri

1. Grafik fungsi baku 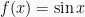$f(x) = \sin x$ ; $f(x) = \cos x$ ; & $f(x) = \tan x$

Sinus

grafik fungsi sinus baku

Kosinus

grafik fungsi cosinus baku

Tangen

grafik fungsi tangen baku

2. Grafik fungsi 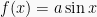$f(x) = a\sin x$ ; $f(x) = a\cos x$ ; & $f(x) = a\tan x$

Didapat dr grafik trigonometri baku dgn cara mengalikan koordinat setiap titik pada grafik baku dgn bilangan a, sedangkan absisnya tetap. Periode grafik tetap $2\pi$ untuk kosinus & sinus. Sedangankan periode tangen $\pi$ .

Sinus

Misalkan $a = 2$ , maka grafiknya :

grafik a sin x

Kosinus

Misalkan $a = 2$ , maka grafiknya

grafik a cos x

Tangen

Misalkan $a = 2$ , maka grafiknya

grafik a tan x

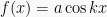3. Grafik fungsi $f(x) = a\sin kx$ ; $f(x) = a\cos kx$ ; & $f(x) = a\tan kx$

Didapat dr grafik trigonometri baku dgn cara mengalikan ordinat setiap titik pada grafik baku dgn bilangan a, sedangkan periode grafik sinus & kosinus menjadi :

$\frac 2\pi \mid k\mid$

Dan tangen

$\frac \pi \mid k\mid$

Sinus

Misalkan $a = 1$ & $k = 2$ , maka grafiknya

a sin 2x

Kosinus

Misalkan $a = 1$ dan $k = 2$ , maka grafiknya

cos 2x

Tangen

Misalkan a=1 $a = 1$ & k=3 $k = 3$ , maka grafiknya

tan 3x

4. Grafik fungsi $f(x) = a\sin(kx\pm b)$ ; $f(x) = a\cos(kx\pm b)$ ; & $f(x) = a\tan (kx\pm b)$ .

Didapat dr grafik trigonometri baku dgn cara mengalikan koordinat setiap titik pada grafik baku dgn bilangan a, sedangkan absisnya digeser sejauh :

$\frac b k$

Jika b konkret, absis digeser kekiri. Dan bila b negatif, absis digeser kekanan. Sedangkan periode grafik sinus & kosinus menjadi :

$\frac 2\pi \mid k\mid$

Dan tangen

$\frac \pi \mid k\mid$

Sinus

Misalkan $a = 1$ , $k = 1$ , & $b = +30^ \circ$ , maka grafiknya

sin kx + b

Kosinus

Misalkan $a = 1$ , $k = 1$ , & $b = -30^ \circ$ , maka grafiknya

cos kx - b

5. Grafik fungsi $f(x) = a\sin (kx\pm b) \pm c$ ; $f(x) = a\cos (kx\pm b) \pm c$ ; & $f(x) = a\tan (kx\pm b) \pm c$ .

Didapat dr grafik trigonometri baku dgn cara mengalikan koordinat setiap titik pada grafik baku dgn bilangan a, sedangkan absisnya digeser sejauh :

$\frac b k$

Jika b nyata, absis digeser kekiri. Dan jikalau b negatif, absis digeser kekanan. Koordinat didapat dgn menggeser titik koordinat grafik baku keatas jikalau c nyata & kebawah jikalau c negatif. Sedangkan periode grafik sinus & kosinus menjadi :

$\frac 2\pi \mid k \mid$

Dan tangen

$\frac \pi \mid k\mid$

Misalkan $a = 1$ , $k = 1$ , $b = 0$ , & $c = 1$ maka grafiknya sinusnya:

grafik fungsi trigonometri a sin x + b

Contoh Soal Grafik Fungsi Trigonometri & Pembahasan

Contoh Soal 1

Fungsi $y = 10\sin x - 4$ . Tentukan nilai maksimum, minimum, & amplitudo fungsi tersebut.

Pembahasan

$y = 10\sin x - 4$

$y_ maks = \mid 10\mid + (-4) = 6$

$y_ min = -\mid 10\mid + (-4) = -10 - 4 = -14$

$Amplitudo = \frac 1 2 (y_ maks - y_ min ) = \frac 1 2 (6 -(-14)) = 10$

Contoh Soal 2

Tentukan nilai maksimum & minimum fungsi $f(x) = 8\sin (x+\frac 3\pi 2 ) \cos x$

Pembahasan

Gunakan : $2\sin a \cos \beta = \sin(a + \beta) + \sin (a - \beta)$

$f(x) = 8\sin(x+\frac 3\pi 2 ) \cos x$ $f(x) = 4 \times 2\sin(x+\frac 3\pi 2 ) \cos x$

$f(x) = 4(\sin(x+\frac 3\pi 2 - x))$

$f(x) = 4(\sin(2x+\frac 3\pi 2 ) + \sin(\frac \pi 2 )) = 4(\sin(2x+\frac 3\pi 2 ) - 1)$

$f(x) = 4\sin (2x+\frac 3\pi 2 ) - 4$

Sehingga :

Untuk sin⁡ $(2x +\frac 3\pi 2 ) = 1$ , maka $f_ maks = 4(1) - 4 = 0$

Untuk sin⁡ $(2x+\frac 3\pi 2 ) = -1$ , maka $f_ min = 4(-1) - 4 = -8$

Contoh Soal 3

Bagilah sudut lancip α menjadi 2 bab, sehingga hasil perkalian kosinus-kosinusnya meraih nilai maksimum.

Tentukan nilai maksimum itu.

Pembahasan

Misalkan 2 bagian sudut yakni x & α-x, maka f(x)=cos⁡x cos⁡(α-x). Berdasarkan rumus trigonometri $2\cos a \cos \beta = \cos (a+\beta) + \cos (a -\beta)$ , maka :