Limit Fungsi -

Daftar Isi

Pengertian Limit Fungsi

Limit merupakan suatu desain matematika dimana sesuatu dikatakan “nyaris” atau “mendekati” nilai suatu bilangan tertentu. Limit dapat berupa sebuah fungsi yg kodomainnya “hampir” atau “mendekati” nilai suatu bilangan orisinil tertentu.

Ilustrasi limit. Sumber gambar: betterexplained.com

Lihat pula materi Sosiologiku.com lainnya:

Suku Banyak

Bunga Tunggal & Bunga Majemuk

Limit Fungsi Aljabar

Dalam pengoperasian limit fungsi aljabar, terdapat beberapa hukum atau teorema limit yg perlu diamati. Jika k konstanta, fungsi f dan fungsi g yakni fungsi-fungsi mempunyai nilai limit yg mendekati bilangan c, maka:

No	TEOREMA
1	$\lim \limits_ x\to c k=k$
2	$\lim \limits_ x\to c x = c$
3	$k \cdot \lim \limits_ x\to c f(x)$
4	$\lim \limits_ x \to c ( f(x) + g(x) )$ $= \lim_ x\to c f(x) + \lim_ x\to c g(x)$
5	$\lim \limits_x\to c( f(x) - g(x) ) = \lim_x\to c f(x) - g(x)$ $= \lim_x \to c f(x) - \lim_ x \to c g(x)$
6	$\lim \limits_ x\to c ( f(x) \cdot g(x) ) = \lim_ x\to c f(x) \cdot \lim_ x\to c g(x)$
7	$\lim \limits_ x\to c \frac f(x) g(x) = \frac \lim_ x\to c f(x) \lim_ x\to c g(x)$
8	$\lim \limits_ x\to c (f(x)^n) = (\lim_ x\to c f(x))^n$
9	$\lim \limits_ x\to c (\sqrt[n] f(x) ) = \sqrt[n] \lim_ x\to c f(x)$

Ada tiga metode dlm melakukan limit fungsi aljabar, yaitu:

1. Metode substitusi

Metode paling gampang dgn memilih hasil suatu limit fungsi adalah dgn mensubstitusi langsung nilai kedalam fungsi f(x). Syarat tata cara ini adalah bila hasil substitusi tak membentuk nilai “tak tentu”. Contoh:

$\lim \limits_ x\to 3 \frac x^2 - 4 x + 2 = \frac 9 - 4 3 + 2 = 1$

2. Metode pemfaktoran

Jika pada metode substitusi menciptakan suatu nilai bentuk tak pasti seperti:

∞, $\frac 0 0$ , $\frac \infty \infty$ , 0 x∞, ∞ – ∞, 0⁰, ∞⁰, atau ∞^∞

maka fungsi tersebut mesti difaktorkan terlebih dahulu sehingga bentuknya tak menjadi bentuk tak tentu, baru lalu mampu disubstitusikan $x\to c$ . Contoh:

$\lim \limits_ x\to 3 \frac x^2 - 3x 2x - 6 = \frac x(x - 3) 2(x - 3) = \frac 3 2$

3. Metode perkalian dgn akar sekawan

Metode ini dipakai bila pada tata cara substitusi langsung menciptakan nilai limit yg irasional. Fungsi dikalikan dgn akar sekawannya biar bentuk limit tersebut tak irasional, sehingga mampu dilakukan kembali substitusi eksklusif nilai $x\to c$ . Contoh:

$\lim \limits_ x\to -1 \frac x +1 1 - \sqrt x + 2 x (\frac 1 + \sqrt x +2 1 + \sqrt x + 2 ) = \frac (x + 1)(1 + \sqrt x+ 2 ) 1 - (x + 2)$

$=\frac (x + 1)(1+\sqrt x+2 ) -x - 1 = \frac (x+1)(1+\sqrt x+2 ) -(x+1) = -(1 + \sqrt x + 2 )$

$=-(1 + \sqrt -(1) + 2 ) = -(1 + 1) = -2$

Dalam pengoprasian limit fungsi aljabar, kadang-kadang nilai x mendekati tak berhingga (∞), sehingga bila disubstitusikan fungsi menciptakan nilai tak tentu. Dalam pengoperasian limitnya, terdapat beberapa aturan atau teorema limit yg perlu diperhatikan. Jika n yaitu bilangan bulat, k konstanta, fungsi f dan fungsi g ialah fungsi-fungsi memiliki nilai limit yg mendekati bilangan c, maka:

No	TEOREMA	SYARAT
1	$\lim \limits_ x\to \infty k = k$	k yaitu konstanta
2	$\lim \limits_ x\to \infty x^n = \infty$
2	$\lim \limits_ x\to \infty \frac 1 x^n = 0$
3	$\lim \limits_ x\to -\infty \frac 1 x^n = \infty$	Jika n = genap
3	$\lim \limits_ x\to - \infty \frac 1 x^n = - \infty$	Jika n = ganjil
4	$\lim \limits_ x\to \infty k \cdot f(x) = k \cdot \lim \limits_ x\to \infty f(x)$	k yaitu konstanta
5	$\lim \limits_ x\to \infty ( f(x) + g(x) ) = \lim \limits_ x\to \infty f(x) + \lim \limits_ x\to \infty g(x)$ $\lim \limits_ x\to \infty f(x) + g(x) = \lim \limits_ x\to \infty f(x) + \lim \limits_ x\to \infty g(x)$
6	$\lim \limits_ x\to \infty ( f(x) - g(x) )$ $= \lim \limits_ x\to \infty f(x) - \lim \limits_ x\to \infty g(x)$
7	$\lim \limits_ x\to \infty ( f(x) \cdot g(x) ) = \lim \limits_ x\to \infty f(x) \cdot \lim \limits_ x\to \infty g(x)$
8	$\lim \limits_ x\to \infty \frac f(x) g(x) = \frac \lim \limits_ x\to \infty f(x) \lim \limits_ x\to \infty g(x)$
9	$\lim \limits_ x\to c (f(x)^n) = (\lim \limits_ x\to c f(x))^n$
10	$\lim \limits_ x\to c (\sqrt[n] f(x) ) = \sqrt[n] \lim \limits_ x\to c f(x)$
11	$\lim \limits_ x\to \infty \frac 1 f(x) = \infty$	$\lim \limits_ x\to \infty f(x) = 0$
11	$\lim \limits_ x\to \infty \frac 1 f(x) = 0$	$\lim \limits_ x\to \infty f(x) = \infty$

Ada dua metode dlm melakukan limit fungsi aljabar bentuk tak berhingga:

Membagi dgn pangkat tertinggi

Metode ini digunakan pada limit fungsi bentuk $\lim \limits_ x\to \infty \frac f(x) g(x)$ . Metode ini dapat dilakukan dgn membagi pembilang f(x) & penyebut g(x) dgn variabel xⁿ berpangkat tertinggi yg ada dlm fungsi f(x) & g(x). Setelahnya, gres dapat disubstitusi dgn $x\to \infty$ . Contoh:

$\lim \limits_ x\to \infty \frac 4x-1 x^2+2 = \frac \frac 4x x^2 - \frac 1 x^2 \frac x^2 x^2 + \frac 2 x^2 = \frac \frac 4 x - \frac 1 x^2 1+\frac 2 x^2 = \frac 0 1 = 0$

Mengalikan bentuk sekawan

Metode ini digunakan pada limit fungsi bentuk $\lim \limits_ x\to \infty f(x) - \lim \limits_ x\to \infty g(x)$ . Metode ini mampu diselesaikan dgn perkalian bentuk sekawan:

$\frac \lim \limits_ x\to \infty f(x)+\lim \limits_ x\to \infty g(x) \lim \limits_ x\to \infty f(x)+\lim \limits_ x \to \infty g(x)$

lalu dilanjutkan pembagian dgn metode pertama yakni membagi dgn pangkat tertinggi. Contoh:

$\lim \limits_ x\to \infty (\sqrt x^2 + 4x - 5 - \sqrt x^2 -x -2 )$

$=\lim \limits_ n\to \infty (\sqrt x^2 + 4x -5 - \sqrt x^2 - x - 2 )$ $x \frac (\sqrt x^2+4x-5 + \sqrt x^2 - x - 2 ) (\sqrt x^2+4x-5 + \sqrt x^2-x-2 )$

$= \lim \limits_ n\to \infty \frac ((x^2+4x-5) - (x^2-x-2)) (\sqrt x^2+4x-5 + \sqrt x^2-x-2 )$ $= \lim \limits_ n\to \infty frac 5x-3 (\sqrt x^2+4x-5 )+\sqrt x^2-x-2$

Kemudian pembilang & penyebut dibagi x pangkat tertinggi yaitu x¹:

$\lim \limits_ n\to \infty \frac \frac 5x x -\frac 3 x (\sqrt \frac x^2+4x-5 x^2 +\sqrt \frac x^2-x-2 x^2 )$ $= \lim \limits_ n\to \infty \frac 5-\frac 3 x (\sqrt 1+\frac 4 x -\frac 5 x^2 + \sqrt 1-\frac 1 x -\frac 2 x^2 )$

$= \frac (-0 (1+1) = \frac 5 2$

Limit Fungsi Trigonometri

Limit pula dapat dipakai pada fungsi trigonometri. Penyelesaiannya sama dgn fungsi limit aljabar. Namun, biar mengetahui penjalasan berikutnya harus mengerti apalagi dahulu desain dr trigonometri. Penyelesaian dlm limit fungsi ini dlm trigonometri mampu dilakukan dgn melakukan pergantian-pergeseran bentuk sinus, cosinus, & tangen.

Ada tiga bentuk biasa dlm limit fungsi trigonometri, yaitu bentuk :

1. Bentuk 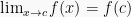$\lim_ x\to c f(x) = f(c)$

Pada bentuk ini, limit dr fungsi trigonometri f(x) merupakan hasil dr substitusi nilai c ke dalam x dari trigonometri. Contoh :

No.	CONTOH	NILAI LIMIT
1	$\lim \limits_ x\to ^\pi/_4 \sin 2x$	$\sin \frac \pi 2$
2	$\lim \limits_ x\to \pi \cos \frac 1 2 x$	$cos\frac 1 2 \pi$
3	$\lim \limits_ x\to ^\pi/_2 \tan x$	$\tan\frac \pi 2$

Jika c = 0, maka rumus limit-limit trigonometrinya ialah selaku berikut :

$\lim \limits_ x\to 0 \sin x = 0$

$\lim \limits_ x\to 0 \cos x = 1$

$\lim \limits_ x\to 0 \cos x = 0$

2. Bentuk $\lim_ x\to c \frac f(x) g(x)$

Pada bentuk ini, limit diperoleh dr perbandingan 2 trigonometri berlawanan. Kedua trigonometri tersebut jikalau pribadi disubstitusi dgn nilai c menciptakan f(c) = 0 & g(c) = 0. Sehingga, nilai limit trigonometri tersebut menjadi bilangan tak pasti $\frac 0 0$ . Penyelesaiannya sama dgn limit fungsi aljabar yakni pemfaktoran. Contoh bentuk ini yaitu:

$\lim \limits_ x\to ^\pi/_2 \frac \sin 2x cosx = \frac 2 \cos x \sin x cosx = 2 \sin x = 2 \sin \frac \pi 2 = 2$

3. Bentuk $\lim_ x\to 0 \frac f(x) g(x)$

Pada bentuk ini, limit diperoleh dr perbandingan antara trigonometri & fungsi aljabar. Jika disubstitusikan eksklusif akan menghaslikan bilangan tak tentu. Pada bentuk ini dijalankan dgn desain turunan. Bentuk rumus dasar limit ini ialah:

$\lim \limits_ x\to 0 \frac \sin x x = \lim_ x\to 0 \frac x \sin x = 1$

$\lim \limits_ x\to 0 \frac x \cos x = 0$

$\lim \limits_ x\to 0 \frac \cos x x = \infty$

$\lim \limits_ x\to 0 \frac \tan x x = \lim_ x\to \frac x \tan x = 1$

Berdasarkan rumus dasar diataas, jikalau dikembangkan menjadi rumus-rumus berikut:

$\lim \limits_ x\to 0 \frac \sin ax bx = \frac a b$

$\lim \limits_ x\to 0 \frac ax \sin bx = \frac a b$

$\lim \limits_ x\to 0 \frac ax \cos bx = 0$

$\lim \limits_ x\to 0 \frac \cos ax bx = \infty$

$\lim \limits_ x\to 0 \frac \tan ax bx = \frac a b$

$\lim \limits_ x\to 0 \frac ax \tan bx = \frac a b$

$\lim \limits_ x\to 0 \frac \sin ax \tan bx = \frac a b$

$\lim \limits_ x\to 0 \frac \tan ax \sin bx = \frac a b$

Contoh Soal Limit Fungsi & Pembahasan

Contoh Soal Limit 1

Tentukanlah nilai dr $\lim_ x\to 2 (\frac 6-x x^2-4 - \frac 1 x-2 )$ (UAN 2002)

Pembahasan 1 :

$\lim \limits_ x\to 2 (\frac 6-x x^2 - \frac 1 x-2 ) = \lim \limits_ x\to 2 (\frac 6-x x^2-4 - \frac x+2 (x-2)(x+2) )$ $= \lim \limits_ x\to 2 \frac (6-x) - (x+2) (x-2)(x+2)$

$=\lim \limits_ x\to 2 \frac 4-2x (x-2)(x+2) = \lim \limits_ x\to 2 \frac -2(x-2) (x-2)(x+2)$ $= \lim \limits_ x\to 2 \frac -2 (x+2)$

$=-\frac 2 4 = -\frac 1 2$

Contoh Soal Limit 2

Tentukanlah nilai dr $\lim \limits_ x\to \infty (\frac \sqrt 4x+x^2 - \sqrt 2+x^2 3x )$ (UN 2009)

Pembahasan 2:

$\lim \limits_ x\to \infty (\frac \sqrt 4x+x^2 -\sqrt 2+x^2 3x ) = \lim_ x\to \infty (\frac \sqrt \frac 4 x^2 +\frac x^2 x^2 -\sqrt \frac 2 x^2 +\frac x^2 x^2 \frac 3x x )$ $= \lim_ x\to \infty (\frac \sqrt \frac 4 x^2 +1 -\sqrt \frac 2 x^2 +1 3 )$

$=(\frac 1-1 3 ) = \frac 0 3 = 0$

Contoh Soal Limit 3

Tentukanlah nilai dr $\lim \limits_ x\to 0 (\frac x^2+ \sin x \tan x 1- \cos 2x )$ (SPMB 2002)

Pembahasan 3 :

$\lim \limits_ x\to 0 (\frac x^2+ \sin x \tan x 1- \cos 2x ) = \lim \limits_ x\to 0 (\frac x^2+ \sin x \tan x 2sin^2x )$ $= \lim \limits_ x\to 0 (\frac x^2 2 \sin^2x +\frac \sin x \tan x 2sin^2x )$